我们来研究一个连续的函数g(x),假设:
我们以下面的函数为例进行研究,其空域和频域的形式如下:
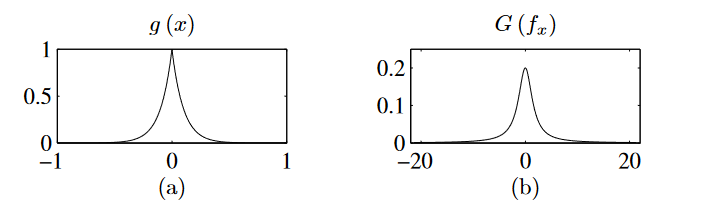
\begin{gathered}g\left(x\right)=\exp\left(-a\left|x\right|\right)\\G\left(f_{x}\right)=\frac1a\frac2{1+\left(2\pi f_{x}/a\right)^{2}}\end{gathered}
连续FT变换对的图像为(这里只显示了部分,空域只显示了[-1,1],频域只显示了[-20,20]):
对DFT来说,在计算过程中,与连续FT不同的有三个地方:
- 首先需要对g(x)进行离散采样(这里以\delta=0.0375为例子)
- 然后需要对g(x)的采样长度进行限制(这里以[-0.2,0.2]为例子)
- 在进行变换后,在频域,还需要对频域进行离散采样。
我们来一步步分析这些操作对信号的影响:
- 首先是对g(x)进行离散采样(这里以\delta=0.0375为例子)
g\left(x\right)\frac1\delta comb\left(\frac x\delta\right)\Leftrightarrow G\left(f_x\right)\otimes\mathrm{comb}\left(\delta f_x\right).
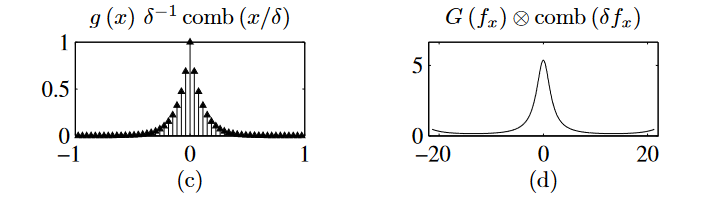

离散采样导致频域信号在频域中的周期性复制,这导致频域发生混叠,对高频成分影响较大。(图中的区间其实是很大很大的,只是仅仅显示了一小部分)
- 然后需要对g(x)的采样长度(采样数)进行限制(这里以[-0.2,0.2]为例子)
g\left(x\right)\frac1\delta comb \left(\frac x\delta\right)\text{rect}\left(\frac xL\right)\Leftrightarrow G\left(f_x\right)\otimes\text{comb}\left(\delta f_x\right)\otimes\left[L\text{ sinc}\left(Lf_x\right)\right].
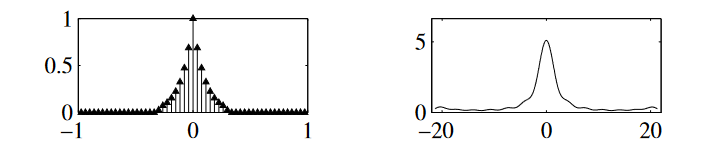

该操作,导致频域卷积一个sinc函数,导致信号的起伏和模糊。
在进行变换后,在频域,还需要对频域进行离散采样。
\widetilde{g}\left(x\right)=\left[g\left(x\right)\frac{1}{\delta}\cosh\left(\frac{x}{\delta}\right)\mathrm{rect}\left(\frac{x}{L}\right)\right]\otimes\left[\frac{1}{L}\cosh\left(\frac{x}{L}\right)\right]
\widetilde{G}\left(f_x\right)=\left[G\left(f_x\right)\otimes\operatorname{comb}\left(\delta f_x\right)\otimes L\operatorname{sinc}\left(Lf_x\right)\right]\times\operatorname{comb}\left(Lf_x\right).
这虽然是对频域的操作,但是同样也会影响空域的解析解
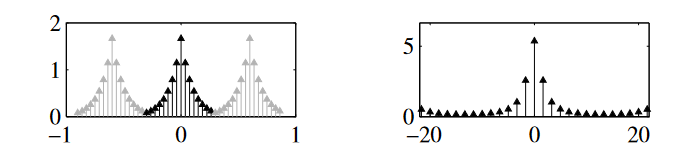

该采样结果导致,空域的信号,在空域中虚拟的赋值,虚拟是因为周期性赋值的区域中,并没有真正的样本。
需要说明一点,这里的频域的采样数是无限多的,实际上,如果考虑IFT的话,我们应该该对频域乘上一个矩形函数,来限制采样数,这样的话,对空域的影响和前面类似,都是一个sinc函数对原空域函数进行了卷积,导致空域信号产生起伏和模糊。
但是真正应该输出的,应该为:

